 إحصائية العضو إحصائية العضو | الجنس :  | | المساهمات : 218 | | نقاط : 650 | | السمعة : 0 |
| |  موضوع: اليكم احبتي دروس الجذع المشترك .. " تم تهييء كل الدروس " موضوع: اليكم احبتي دروس الجذع المشترك .. " تم تهييء كل الدروس "  اليكم احبتي دروس الجذع المشترك .. " تم تهييء كل الدروس " اليكم احبتي دروس الجذع المشترك .. " تم تهييء كل الدروس " بسم الله الرحمان الرحيم
اخي الكريم ، اختي الكريمة
ساقدم لكم اليوم ان شاء الله عُصارةً للجذع المشترك
و ذلك عن طريق دروس شاملة
لذلك قدِّروا مجهودي و لا تبخلوا علي بالردود
"ساضع الدروس واحدة واحدة و ليس في نفس اليوم لان ذلك عسير جدا
لذا ساضع درسا او اثنين في اليوم"
على بركة الله1-الرياضيات
مجموعة الأعداد الصحيحة الطبيعية و مبادئ في الحسابيات
القدرات المنتظرة
*- توظيف الزوجية وتفكيك عدد إلى جداء عوامل أولية في حل بعض المسائل البسيطة
حول الأعداد الصحيحة الطبيعية.
-I-مجموعة الأعداد الصحيحة الطبيعية :
-1 مجموعة الأعداد الصحيحة الطبيعية:
*نشاط*
من بين الأعداد التالية حدد تلك التي تمثل أعدادا صحيحة طبيعية:5 ; 4+16 ; 5/2 ; 12-23 ; 15/3 ; 2.15
*تعريف*
الأعداد 0 , 1 , 2 , 3 , 4 , 5 , 6 , .... , n ;تسمى أعدادا صحيحة طبيعية و
تكون مجموعة تسمى مجموعة الأعداد الصحيحة الطبيعية نرمز لها ب .N نكتب ( 0 , 1 , 2 , ....)=N مصطلحات و ترميز
*- العدد 0 يسمى العدد الصحيح الطبيعي المنعدم
*- مجموعة الأعداد الصحيحة الطبيعية الغير المنعدمة نرمز لها بالرمز *N
2-الأعداد الزوجية – الأعداد الفردية:
*تعريف*
- نقول إن العدد الصحيح الطبيعي a عدد زوجي إذا وفقط آان يوجد عدد صحيح
طبيعي k حيث : a=2k-نقول إن العدد الصحيح الطبيعي a عدد فردي إذا وفقط آان
يوجد عدد صحيح طبيعي k حيث a=2k+1
*أمثلة*
الأعداد 0 , 2 , 4 , 6 , 8 , .. أعداد زوجية
الأعداد 1 , 3 , 5 , 7 , 9 .....أعداد فردية
*ملاحظات*
*- العدد الصحيح الطبيعي هو إما عدد زوجي أو عدد فردي
*- مجموع عددين زوجيين هو عدد زوجي
*-مجموع عددين فرديين هو عدد زوجي
*-مجموع عدد زوجي و عدد فردي هو عدد فردي
II- مضاعفات عدد – قواسم عدد :1-مضاعفات عدد:
*تعريف*
ليكن a و b عددين صحيحين طبيعيين حيث b غير منعدم
نقول إن العدد a مضاعف للعدد b إذا وفقط إذا وجد عدد صحيح طبيعي k حيث a=bk
*أمثلة*
- الأعداد 0 , 5 , 10 , 15 ... 1755 مضاعفات للعدد 5
-22 ليس مضاعف للعدد 4
* ليكن b عنصراً من *N
0×k =0
مضاعفات b هي الأعداد kb حيث k ينتمي الى N
*خاصية*
* لكل عدد صحيح طبيعي غير منعدم ما لنهاية من المضاعفات
* للعدد 0 مضاعف وحيد هو 0*المضاعف المشترك الأصغر*
ليكن a و b عددين صحيحين طبيعيين غير منعدمين
المضاعف المشترك الأصغر للعددين a و b هو أصغر مضاعف مشترك غير منعدم للعددين a و b نرمز له بالرمز ppcm
أمثلة
ppcm (4;9) = 36
ppcm (6;10)=30
-2قواسم عدد:
*تعريف*
ليكن a و b عددين صحيحين طبيعيين حيث b غير منعدم
نقول إن العدد b قاسم للعدد a إذا وفقط إذا وجد عدد صحيح طبيعي k حيث a=bk
*ملاحظة*
العدد b قاسم للعدد a إذا وفقط إذا العدد a مضاعف للعدد b
-آلعدد آلصحيح آلطبيعي غير منعدم مخالفا ل 1 له على الاقل قاسمان 1 و نفسه
- للعدد 1 قاسم وحيد هو نفسه
-جميع الأعداد الصحيحة الطبيعية الغير المنعدمة تقسم 0
نقول أيضا العدد a قابل للقسمة على b
*القاسم المشترك الأآبر لعددين*
تعريف:
ليكن a و b عددين صحيحين طبيعيين غير منعدمين
القاسم المشترك الأآبر للعددين a و b هو اآبر قاسم مشترك لهما
نرمز له بالرمز pgcd
مثال:
pgcd(126;90)=18
pgcd(4;9)=1
III-الأعداد الأولية :1- تعريف:
نسمي عددا أوليا آل عدد صحيح طبيعي له قاسمان بالضبط
*أمثلة*
-حدد الأعداد الأولية الأصغر من 40الأعداد الأولية الأصغر من 40 هي: 2,3,7,11,13,17,19,23,29,31,372-التفكيك إلى جداء عوامل أولية لعدد غير أولي مبرهنة (مقبولة 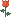
كل عدد صحيح طبيعي n هو عدد أولي أو جداء عوامل أولية .
أمثلة:
تعريف: 41 عدد أولي 72 عدد غير أولي و 72 = 8×9 = 3×3×2×2×2
ليكن a عددا صحيحا طبيعيا غير أولي
كتابة a على شكل جداء عوامله أولية تسمى " التفكيك إلى جداء عوامل أولية" للعدد a
فكك الأعداد 24;319;1344 إلى جداء عوامل أوليةأمثلة: 24=8×3=2×2×2×3 319=11×29 1344=4×4×4×21=2×2×2×2×2×2×3×7
تقنية للتفكيك
-لتفكيك عدد صحيح طبيعي غير منعدم a نأخذ اصغر عدد أولي يقسم a و ننجز
القسمة فنحصل على عدد b خارج القسمة فنأخذ اصغر عدد أولي يقسم b فنحصل على
خارج القسمة .......و نتابع على هذا المنوال حتى نحصل على خارج يساوي 1 .
العدد a سيكون هو جداء جميع الأعداد الأولية التي قسمنا بها .
إضافات
* طريقة لتحديد المضاعف المشترك الأصغر للعددين a و b حيث a>bأحدد مضاعفات a ثم أتآكد بالتتابع ابتداء من أصغر مضاعف غير منعدم للعدد a هل هو مضاعف للعدد b , فإذا آان الجواب لا ، أتابع البحث إن آان نعم ، أتوقف و العدد الذي حصلت فيه على هذا الجواب هو المضاعف المشترك الأصغر للعددين a و b .
**طريقة لتحديد القاسم المشترك الآكبر للعددين a و b حيث a>b
أحدد قواسم العدد b ثم أتآكد بالتتابع تناقصيا ابتداء من أآبر قاسم للعدد b هل هو قاسم للعدد a فإذا آان الجواب لا ، أتابع البحث ان آان نعم ، أتوقف و العدد الذي حصلت فيه على هذا الجواب هو القاسم المشترك الأآبر للعددين a و b .
***طريقة لتحديد ما إذا كان العدد a أوليا أم لا
نحدد أولا جميع الأعداد الأولية p حيث p×p
-إذا كان a يقبل القسمة على أحد هذه الأعداد فان a غير أولي
-إذا كان a لا يقبل القسمة على أي عدد من هذه الأعداد فان a أولي
| اقتباس: |
المجموعات: IN; IR;Q;Z;ID
1-مجموعة الأعداد الصحيحة النسبية :
*مجموعة الأعداد الصحيحة الطبيعية هي (..., IN=(0,1,2,3,4
آل عدد صحيح طبيعي هو عدد صحيح نسبي
نقول ان المجموعة IN جزء من المجموعة Z أو المجموعة IN ضمن المجموعة Z
2-مجموعة الأعداد العشرية النسبية:
*تعريف:كل عدد له كتابة كسرية على شكل a/10 n
*نتائج:
-العدد العشري له آتابة بعدد منته من الأرقام على يمين الفاصلة
-كل عدد صحيح نسبي a هو عدد عشري نسبي
*تعريف*
العدد الجدري هو كل عدد يمكن كتابته على شكل a/b حيث a ينتمي الى Z و b ينتمي الى Z و b يخالف الصفر
يرمز لمجموعة الاعداد الجذرية بQ
-3/7 عدد جذري ; 6 عدد جذري ; -1.36 عدد جذري ; جذر 3 ليس عددا جذريا.
الاعداد الجذرية و الاعداد لا جذرية تكون مجموعة تسمى مجموعة الاعداد الحقيقية
يرمز لها ب IR
الاعداد الصحيحة الطبيعية و مقابلاتها تكون مجموعة الاعداد الصحيحة النسبية يرمز لها بZ
نكتب (... Z=(-3,-2,-1,0,1,2,3
ملاحظة:
نرمز لمجموعة الاعداد العشرية النسبية ب ID
3-مجموعة الأعداد الجذرية:
4-مجموعة الأعداد الحقيقية:
|
| اقتباس: |
الترتيب في IR
*تعريف:
ليكن a و b عددين حقيقيين
a>b يعني a-b>0
a<0
* خاصيات و نتائج:
ليكن a و b و c و d أعداد حقيقية
إذاكان a>b و b>c فان a>c
x,b,a أعداد حقيقية حيث a≤x≤b
a+b/2 قيمة مقربة للعدد x بالدقة a-b/2
*المجالات:
مجموعة الاعداد
حيث: ترميزها قراءة و تمثيل على المستقيم X الحقيقية
a;b] a≤x≤b
a;b[ a≺x≺b
a;b[ a≤x≺b
a;b] a≺x≤b
a;+∞[ a≤x
a;+∞[ a≺x
]−∞,b] x ≤ b
]−∞;b[ x ≺ b
b مفتوح في b ، يقرأ المجال ناقص لانهاية
*القيمة المطلقة :
-ليكن Δ(O;I مستقيما مدرجا
القيمة المطلقة لكل عدد حقيقي x هي المسافة بين النقطة M التي أفصولها x و النقطة o .
إذاكان a>b فان a+c>b+c
إذاكان a> b و c>d فان a+c>b+d
إذاكان a>b و c>0 فان ac>bc
إذاكان a>b و c<0 فان ac
إذاكان a>b>0 فان a2>b2
إذاكان 0
يقرأ المجال المغلق الذي طرفاه a و b
يقرأ المجال المفتوح الذي طرفاه a وb
يقرأ المجال المفتوح على اليمين الذي طرفاه a و b
يقرأ المجال المفتوح على اليسار الذي طرفاه a و b
يقرأ المجال زائد ما لانهاية مغلق في a
يقرأ المجال زائد ما لانهاية مفتوح في a
مغلق في b ، يقرأ المجال ناقص لانهاية
ليكن x من IR
إذاكان x>0 فان x=x
إذاكان x<0 فان x=-x |
| اقتباس: |
المعادلات و المتراجحات من الدرجة الاولى والثانية بمجهول واحد
-جميع حلول معادلة (أو متراجحة) تكون مجموعة تسمى مجموعة حلول المعادلة (أو المتراجحة)
نرمز لها ب S أو S' ....
-نقول ان معادلتين (أو متراجحين) متكافئتان إذا آانت للمعادلتين (أو للمتراجحتين) نفس مجموعة الحلول.
*المعادلة التالفية:
كل معادلة يمكن آتابتها على شكلax+b=0 تسمى معادلة تالفية x∈ IR
*المتراجحات التالفية بمجهول واحد:
آل متراجحة يمكن آتابتها على شكل ax+b≺0 x∈ IR أو ax+b≤0 أو x∈ IR أو ax+b≥0 x∈ IR أو ax+b>0 حيث a,b)∈ IR2
*المعادلات من الدرجة الثانية بمجهول واحد:
نسمي معادلة من الدرجة الثانية في IR كل معادلة على الشكل ax² +bx+c =0
حل المعادلة يتوقف على إشارة العدد b² − 4ac الذي يسمى مميز المعادلة
ax 2 +bx +c =0 نرمز له ب Δ نكتب Δ =b² − 4ac
*إذا كان Δ ≺0 فان المعادلة لا تقبل حلا في IR
**إذا كان Δ =0 فان x=-b/2a
*** إذا كان Δ >0 فان
ax ² + bx +c =0 تكافئ x+b/2a)²-Δ/4a²=0
Δ = 4(b'2 −ac نضع Δ'=b'2−ac
" ان هاته الدروس اهيئها بنفسي من دفتري الخاص لذلك هي
تتطلب مني الوقت"
:thumbs-up[1]:
و تسمى معادلة من الدرجة الأولى بمجهول واحد إذا كان a ≠0
و تسمى متراجحة من الدرجة الأولى بمجهول واحد إذا كان a ≠0
حيث a و b و c أعداد حقيقية و a غير منعدم.
اشارة Δ هي اشارة 'Δ
العدد ' Δ يسمى المميز المختصر للمعادلة
|
|







